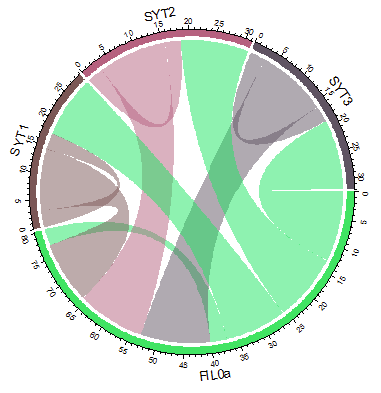
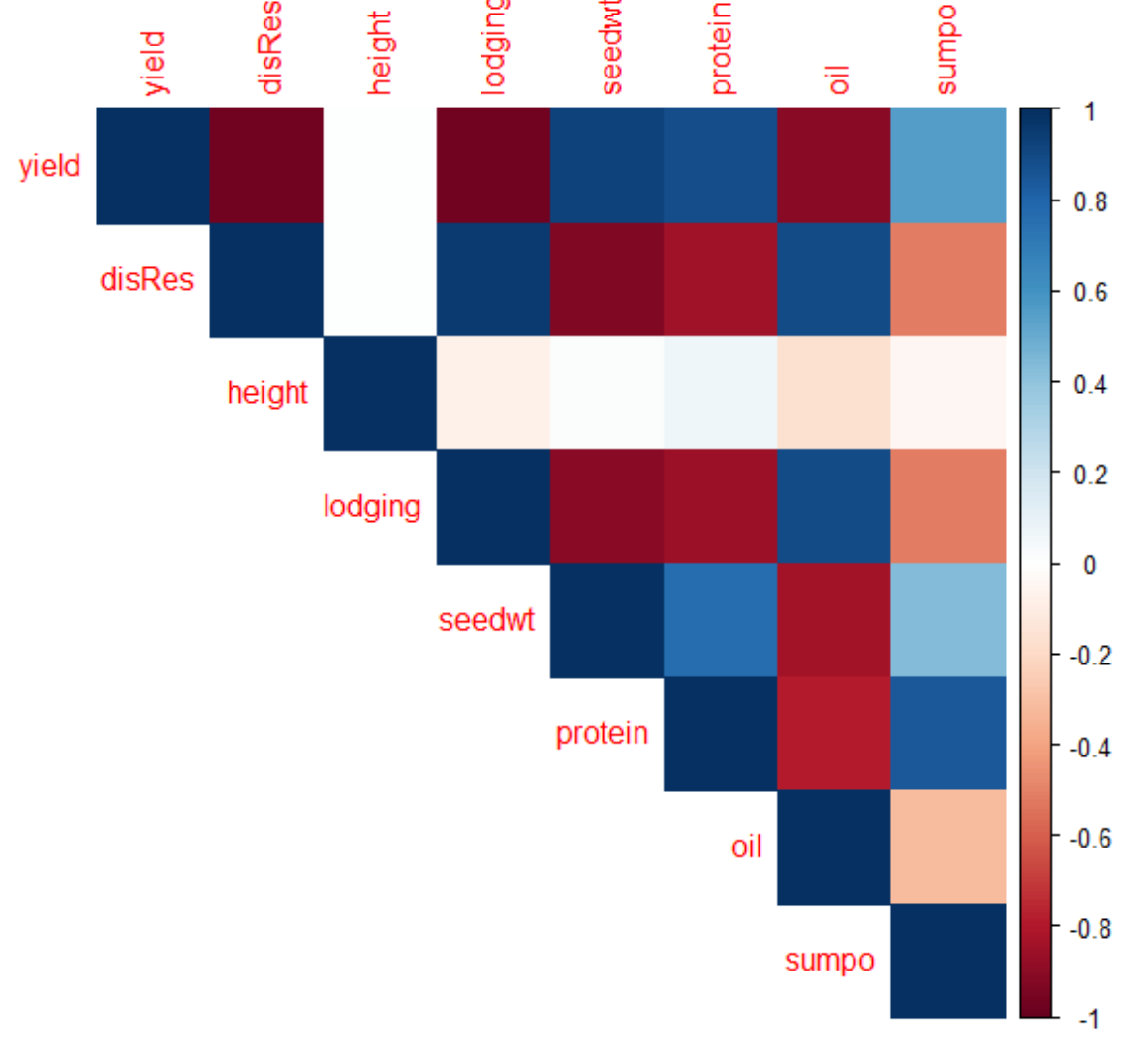
RNA-seq data analysis
Since the availability of the next-generation sequencing (NGS) technology, RNA-seq has become popular in biological research in many species for gene discovery, annotation and expression analysis along with the identification of SNP markers across a genome. Compared with the previous DNA microarray technology, it can provide a comprehensive overview of transcriptome with some of the great advantages including higher sensitivity, higher resolution at nucleotide level and no prerequisite of gene sequences. The advances in high-throughput sequencing with decreasing cost have made it affordable to rapidly generate a large quantity of DNA sequences and genotypic data for investigating a wide range of biological and medical problems. In the meantime, massive and complex sequence datasets generated from the sequencers create a need for the development of statistical and bio-computational applications to tackle the analysis and data management.
Here is a hypothetical example of RNA-Seq dataset from the drought experiment with hybrid maize, i.e. drought stress vs optimal water supply. Samples were sequenced with short reads being mapped onto the maize reference genome and the number of reads mapped to the features of interest (genic regions) were obtained. The gene expression profile for a particular sample consists of the set of gene-wise counts of sequence reads from that sample and one of the experimental objectives is to identify the differentially expressed genes.
As the distribution of direct count data is highly skewed, a log2 transformation can approximately normalize the distributions as indicated below:
} "t = log{_{2}}^{(C + C_{0})}")
where, C is the count data while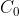 
is a small positive constant (“1", for instance) to facilitate the computation of the logarithm value in case of zero count for some conditions.
The following table lists the top 12 rows of transformed data from the drought experiments:
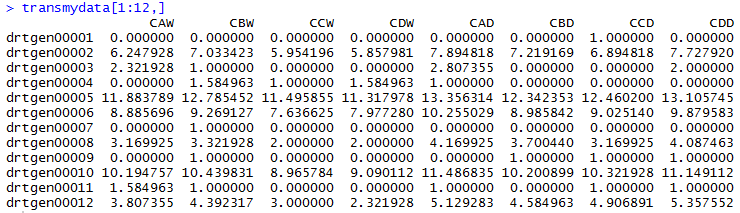
The data set should be performed with additional manipulations to filter and exclude the genes with non-differential expression. A simple scatter plot can be generated using the script below prior to the differential gene expression analysis.
ggplot(data=mydata, aes(x = CAW, y = CAD, color=CBD)) +
geom_point(size=3) +
labs(title="Scatterplot of log2 transformed gene expression data \nfrom the drought experiment of hybrid corn", x= "Log2 gene expression for CAW", y="Log2 gene expression for CAD") +
theme(
plot.title = element_text(color="#0000ff", hjust = 0.5, size=13, face="bold"),
axis.title.x = element_text(color="#003366", size=12, face="bold"),
axis.title.y = element_text(color="#003366", size=12, face="bold"))
Then, an MA plot for differential expression analysis can be created to visualize the differences between measurements obtained from two samples or treatments based on the log-intensity ratio (M) and the average log-expression (A).
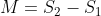
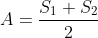
where,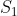 
and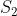 
are the expression data for sample 1 and 2, respectively.
ggplot(data=mydata, aes(x = A, y = M, color=CBD)) +
geom_point(size=3) +
labs(title="MA-plot for log2 transformed gene expression data \nfrom the drought experiment of hybrid corn", x= "Log2 mean expression", y="Log2 fold change\n(drought condition vs optimal water supply)") +
theme(
plot.title = element_text(color="#0000ff", hjust = 0.5, size=13, face="bold"),
axis.title.x = element_text(color="#003366", size=12, face="bold"),
axis.title.y = element_text(color="#003366", size=12, face="bold"))
To generate a heatmap for clustering gene expression leveles across samples and treatments:
library(stats)
library(gplots)
heatmap.2(as.matrix(mydata), col=redgreen(95), scale="row", key=T, keysize=1.5,density.info="none",
trace="none", cexCol=0.9, labRow=NA)
The transformed dataset can be normalized using the following approach (minmax normalization):
}{max(x)-min(x)} "x_{i}^{'} = \frac{x_{i}-min(x)}{max(x)-min(x)}")
where,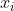 
and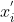 
are the 
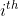data before and after normalization, respectively.
Thus, a heatmap of similarities can also be created among the participating genotypes based on the expressed genes under different treatment conditions:
library(RColorBrewer)
mydata = as.matrix(dist(t(mydata)))
mydata = (mydata - min(mydata))/(max(mydata) - min(mydata))
hmcol = colorRampPalette(brewer.pal(9, "GnBu"))(100)
heatmap(mydata, col=hmcol)
